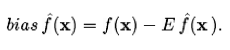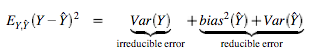In [1] Pedro Domingos recopilates some Machine Learning related stuff that can be useful for a beginner in the field. There is a list of journals
- Machine Learning
- Journal of Artificial Intelligence Research
- Neural Computation
- IEEE Transactions on Pattern Analysis and Machine Intelligence
- Journal of Machine Learning Research
- Journal of Machine Learning Gossip
- International Conference on Machine Learning
- European Conference on Machine Learning
- International Joint Conference on Artificial Intelligence
- National Conference on Artificial Intelligence
- European Conference on Artificial Intelligence
- Annual Conference on Neural Information Processing Systems
- International Workshop on Multistrategy Learning
- International Workshop on Artificial Intelligence and Statistics
- International Conference on Computational Learning Theory (COLT)
- European Conference on Computational Learning Theory
- UCI repository of machine learning databases
- Online bibliographies of several subareas of machine learning
- Machine Learning List
- AI and Statistics List
- MLC++
- Weka
- Citeseer
- DBLP
- Rexa
- DataSets for Data Mining and Knowledge Discovery
- DataMining Conferences
- Machine Learning (Theory)
References:
[1] Pedro Domingos, "E4 - Machine Learning" In W. Klosgen and J. Zytkow (eds.), Handbook of Data Mining and Knowledge Discovery (pp. 660-670), 2002. New York: Oxford University Press. (Download)