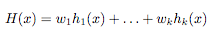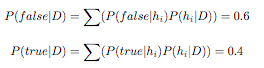Ensemble methods are methods than rather than finding one best hypothesis for the learning problem construct a set of hypotheses (called "committee" or "ensemble") that can, in some fashion, "vote" to predict the class of the new data example. As defined in [1], "an ensemble method constructs a set of hypothesis {h1, . . . , hk}, chooses a set of weights {w1, . . . , wk} and constructs the "voted" classifier
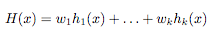
The classification decision of the combined classifier is +1 if H(x) >= 0 y -1 otherwise"
Ensemble learning algorithms work running a base learning algorithm multiple times, generating a hypothesis at each iteration. The hypothesis can be generated in two ways
1) In a independent way, resulting in a set of diverse hypothesis. It can be done by running the algorithm several times and providing different training data at each iteration or providing different subsets of the input features at each iteration. An example of this way is Bagging [2].
2) In an additive way, adding one hypothesis at a time to the ensemble, and constructing the hypothesis trying to minimize the classification error on a weighted training data set. An example of this way is Boosting [3], [4].
Bagging (“Bootstrap Aggregatting”)
Given a training data with m examples, Bagging works by generating at each iteration a new training data set of m examples by sampling uniformly from the original examples, which means some original examples appear multiple times and other original examples do not appear in the resampling. If the learning algorithm is unstable (small changes in the training data causes large changes in the hypothesis, like decision trees) then Bagging will produce a set of diverse hypothesis (H).
Having H, for classifying a new example, we should proceed to a voting between all the hypothesis hi belonging to H, and the final classification would be the most voted one.
Boosting
Boosting assings a weight to each training sample and then, at each iteration, generates a model that tries to minimize the sum of the weights of the misclassificated examples. The errors at each iteration are used to actualize the weights of the training samples, increasing the misclasificated instances’ weights and decreasing the correctly classificated instances’ weights.
¿Why use Ensembles?
[5] gives a good justification of ensemble using.
- "The first cause of the nees for ensembles is that the trainning data may not provide sufficient information for choosing a single best classifier from H. Most of our learning algorithms consider very large hypothesis spaces, so even after eliminating hypotheses that misclassify training examples, there are many hypothesis remaining".
- "A second cause...is that our learning algorithms may not be able to solve the difficult search problems that we pose"
- "A third cause...is that our hypothesis space H may not contain the trus function f"
Basic References
[1] Dietterich, T. G. (2002). "Ensemble Learning." In The Handbook of Brain Theory and Neural Networks, Second edition, (M.A. Arbib, Ed.), Cambridge, MA: The MIT Press, 2002. 405-408. (
Download)
Specific References
[2] Breiman, L. (1996a), "Bagging Predictors", Machine Learning, Vol. 24, No. 2, pp. 123-140. (
Download)
[3] Yoav Freund and Robert E. Schapire. "Experiments with a new boosting algorithm." In Machine Learning: Proceedings of the Thirteenth International Conference, pages 148-156, 1996. (
Download)
[4] J. R. Quinlan, "Bagging, Boosting, and C4.5 (1996)", AAAI/IAAI, Vol. 1 (
Download)
Other References:
[5] Dietterich, T. G, "Machine Learning: Four Current Directions" (1997) (
Download)
Ensemble Learning Researchers: