When trying to select a model that explains the data, we usually select (from all the possible models) the one which better fits the data. But sometimes we have some model that explains really well the data, creating a model selection uncertainty, which is usually ignored. BMA (Bayesian Model Averaging provides a coherent mechanism for accounting for this model uncertainty, combining predictions from the different models according to their probability.
As an example, consider that we have an evidence D and 3 possible hypothesis h1, h2 and h3. The posterior probabilities for those hypothesis are P( h1 | D ) = 0.4, P( h2 | D ) = 0.3 and P( h3 | D ) = 0.3. Giving a new observation, h1 classifies it as true and h2 and h3 classify it as false, then the result of the global classifier (BMA) would be calculated as follows: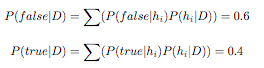
Basic BMA Bibliography
[1] J. A.and Madigan D. Hoeting and A.E.and Volinsky C.T. Raftery. Bayesian model averaging: A tutorial (With Discussion). Statistical Science, 44(4):382--417, 1999. (Download)
Basic BMA Researchers
Go to main |
Go to sidebar
Labels
- amazon (1)
- analysis (1)
- artificial intelligence (2)
- blog (2)
- business intelligence (2)
- cfps (27)
- challenge (1)
- complexity (1)
- conference (9)
- data mining (22)
- dataset (3)
- evaluation (1)
- events (4)
- flickrbabel (1)
- fraud (1)
- google (1)
- industry (1)
- information access (2)
- information retrieval (4)
- internet (2)
- investment (1)
- invitation (1)
- journal (3)
- lectures (1)
- link (1)
- machine learning (12)
- medical (4)
- news (1)
- nlp (2)
- nlp. enterprise (1)
- ontologies (2)
- open access (3)
- open software (1)
- opinion mining (1)
- panel (1)
- people (4)
- performance (2)
- position (1)
- presentation (2)
- recommender systems (6)
- reflection (1)
- research (5)
- resources (1)
- robots (1)
- scholarship (1)
- science (1)
- search (5)
- semantics (3)
- sentiment analysis (1)
- sgp (1)
- smuc (1)
- social media (12)
- social networks (3)
- software (1)
- summer school (2)
- survey (1)
- tags (1)
- talk (1)
- tool (1)
- travel (1)
- web (1)
- wikipedia (1)
- wipley (2)
- workshop (2)

This blog is licensed under Creative Commons
©2006-2008 Social Media, Data Mining & Machine Learning
Disclaimer: put a content dislaimer here - Mauris elit. Donec neque. Phasellus nec sapien quis pede facilisis suscipit. Aenean quis risus sit amet eros volutpat ullamcorper. Ut a mi. Etiam nulla. Mauris interdum.Lorem ipsum dolor sit amet, consectetuer adipiscing elit. Quisque sed felis. Aliquam sit amet felis. Mauris semper, velit semper laoreet dictum, quam diam dictum urna
The Forte theme by Moses Francis
Port to Blogger by Blog and Web and BTemplates
Disclaimer: put a content dislaimer here - Mauris elit. Donec neque. Phasellus nec sapien quis pede facilisis suscipit. Aenean quis risus sit amet eros volutpat ullamcorper. Ut a mi. Etiam nulla. Mauris interdum.Lorem ipsum dolor sit amet, consectetuer adipiscing elit. Quisque sed felis. Aliquam sit amet felis. Mauris semper, velit semper laoreet dictum, quam diam dictum urna
The Forte theme by Moses Francis
Port to Blogger by Blog and Web and BTemplates









1 comments:
This was lovelyy to read
Post a Comment